The quadratic polynomial f1/4
f1/4 is the quadratic ploynomical f(z) = z2 + c, where c≈ -0.228155 + 1.11514 i is a zero of the cubic polynomial c3 + 2c2 + 2c + 2.The notation f1/4 comes from external rays. In the complement of the filled Julia sets, the external ray with angle 1/4 (mod 1) lands at the critical value c. From this it follows that f(c) has angle 1/2 = 2 x 1/4, and f2(c) has angle 1 = 2 x 1/2. Since 2 x 1 ≡ 1 (mod 1), f2(c) is fixed and f has four postcritical points (∞, c, f(c), and f2(c). The Julia set for f1/4 is shown in the figure below, which was created from Mathematica.
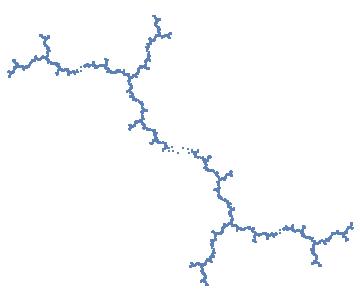
The diagram for f1/4
Input and output files
- f_fourth.input
- f_fourth_Main.output
- f_fourth_MOD.output
- f_fourth_Table.output
- f_fourthMod2Corre.ps
- f_fourthDynPortrait.ps
- f_fourthGraphMu.ps
- f_fourthGraphMuLines.ps
- f_fourthGraphMuTorus.ps
- f_fourthHalfSpace.ps
- f_fourthPrenDgm.ps
- f_fourthSigma.ps
- f_fourthTreeEMOD.ps
- f_fourthTreeMOD.ps
- f_fourthTreePMOD.ps