The basilica mated with the basilica
The basilica polynomial is the polynomial F(z)=z2-1.Critical points of F: 0, ∞
Dynamic portrait: 0 -2-> -1 -1-> 0, ∞ -2-> ∞
There exists an open topological disk in the Riemann sphere containing ∞ stabilized by F on which the action of F is equivalent to the action of z↦ z2 on the open unit disk. Let D be the complement of this open topological disk in the Riemann sphere. Then F stabilizes D. We take two copies of D and identify their boundaries in the straightforward way so that two copies of F combine to obtain the mating f of F with itself.
Critical portrait of f: a -2-> b -1-> a, c -2-> d -1-> c
The diagram for f
According to Kelsey and Lodges' paper ``Quadratic Thurston maps with
few postcritical points'' Geom. Dedicata 201 (2019), 33-55,
especially Tables 2 and 4, every Thurston map with this dynamic
portrait is obstructed. Furthermore these maps are all Thurston
equivalent to twists of any one such map, say f, by powers of a
Dehn twist about the obstruction. The f-pullback of the obstruction
is homotopic to the obstruction, rel Pf={a,b,c,d}, and the same
is true for another homotopy class of curves in S2 -
Pf,
namely, the homotopy class of the equator of the mating. This
property determines the Thurston equivalence class of f among these
Thurston equivalence classes. Now one verifies that the following NET
map presentation diagram yields a NET map with the same dynamic
portrait as f. It has an obstruction with slope ∞ and an
equator with slope 0. It must be Thurston equivalent to f.
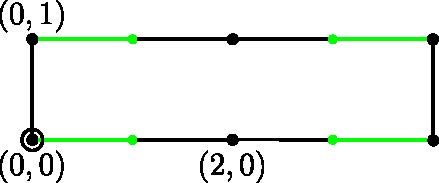
Input and output files
- basilicabasilica.input
- basilicabasilica_Main.output
- basilicabasilica_MOD.output
- basilicabasilica_Table.output
- basilicabasilicaMod2Corre.ps
- basilicabasilicaDynPortrait.ps
- basilicabasilicaGraphMu.ps
- basilicabasilicaGraphMuLines.ps
- basilicabasilicaGraphMuTorus.ps
- basilicabasilicaHalfSpace.ps
- basilicabasilicaPrenDgm.ps
- basilicabasilicaSigma.ps
- basilicabasilicaTreeEMOD.ps
- basilicabasilicaTreeMOD.ps
- basilicabasilicaTreePMOD.ps