Tao Lin's Research
Page
My research
interests involve numerical methods for solving partial differential equations
and integro-differential equations. My recent focus
is the immersed finite element methods for interface problems and their
applications.
A very brief introduction to the immersed finite elements (
In many applications,
we often need to simulate a procedure in a domain consisting of several
materials separated from each other by curves or surfaces. This usually leads
to the so called interface problem which is a boundary value problem of a PDE
whose coefficients are discontinuous across the material interface.
The conventional finite
element methods can be used to solve interface problems, but they usually
require that the each element contains essentially one of the materials.
Geometrically, this means that each element has to be on one side of a material
interface.
The immersed finite
elements are developed such that each element can contain multiple materials so
that elements are allowed to sit on an interface. The basic features of the
immersed finite elements are:
A. Their meshes can be
independent of the interface location; hence, if preferred, structured meshes
can be used to solve a problem with non-trivial interface.
B. The basis
functions on an interface element are formed according the interface jump
conditions.
Some Publications on IFE methods:
n
Guo,
R., Lin, T., and Lin, Y., Error
Estimates For A Partially Penalized Immersed Finite Element, ESAIM Mathematical Modelling and Numerical
Analysis, DOI: 10.1051/m2an/2019051.
n
Guo,
R., Lin, T., A
higher degree immersed finite element method based on a Cauchy extension for
elliptic interface problems, SIAM
Journal on Numerical Analysis, (2019) 57, No. 4, 1545-1573.
n
Adjerid, S., Chaabane,
N., Lin, T., and Yue, P., An
immersed discontinuous finite element method for the Stokes problem with a
moving interface, Journal of
Computational and Applied Mathematics, (2019) 362, 540-559.
n
Lin,
T., Lin, Y., and Zhuang, Q., Solving
Interface Problems of the Helmholtz Equation by Immersed Finite Element Methods,
Communications on Applied Mathematics and
Computation (2019). https://doi.org/10.1007/s42967-019-0002-2
n
Guo,
R., Lin, T., A
group of immersed finite-element spaces for elliptic interface problems, IMA Journal of Numerical Analysis (2019)
39, 482?11.
n
Guo,
R., Lin, T., Lin, Y., Approximation
capabilities of immersed finite element spaces for elasticity Interface
problems, Numerical Methods for
Partial Differential Equations, 35(2019), 1243-1268.
n
Guo,
R., Lin, T., Lin, Y., A
Fixed Mesh Method with Immersed Finite Elements for Solving Interface Inverse Problems,
Journal of Scientific Computing,
79(2019), 148?75.
n
Adjerid, S., Ben-Romdhane,
M., Lin, T., Higher
degree immersed finite element spaces constructed according to the actual
interface, Computers and Mathematics
with Applications, 75 (2018) 1868?881.
n
Guo,
R., Lin, T., Zhang, X., Nonconforming
immersed finite element spaces for elliptic interface problems, Computers and Mathematics with Applications,
75(2018), 2002-2016.
n
Adjerid, S., Guo, R., Lin, T., High
Degree Immersed Finite Element Spaces By A Least Squares Method, International Journal Of Numerical Analysis
And Modeling, 14(2017), 604-626.
n
Lin,
M., Lin, T., Zhang, H., Error
Analysis Of An Immersed Finite Element Method For Euler-Bernoulli Beam
Interface Problems, International
Journal Of Numerical Analysis And Modeling, 14(2017), 822-841.
n
Han,
D., Wang, P., He, X., Lin, T., Wang, J., A
3D immersed finite element method with non-homogeneous interface flux jump for
applications in particle-in-cell simulations of plasma–lunar surface
interactions, Journal of Computational
Physics, 321(2016), 965-980.
n
Adjerid, S., Chaabane,
N., Lin, T., An
immersed discontinuous finite element method for Stokes interface problems,
Computer Methods in Applied Mechanics and
Engineering, 293(2015) 170?90.
n
Lin,
T., Lin, Y., Zhang, X., Partially
Penalized Immersed Finite Element Methods For Elliptic Interface Problems, SIAM Journal on Numerical Analysis,
53(2015), 1121-1144.
n
Adjerid, S., Ben-Romdhane,
M., Lin, T., Higher
Degree Immersed Finite Element Methods For Second-Order Elliptic Interface
Problems, International Journal Of
Numerical Analysis And Modeling, 11(2014), 541-566.
n
He,
X., Lin, T., Lin, Y., A
selective immersed discontinuous Galerkin method for
elliptic interface problems, Mathematical Methods in the Applied Sciences,
37(2014), 983?002.
n
He,
X., Lin, T., Lin, Y., Zhang, X., Immersed
Finite Element Methods for Parabolic Equations with Moving Interface, Numerical Methods for Partial Differential
Equations, 29(2013), 619-646.
n
Lin,
T., Lin, Y., Zhang, X., Immersed
finite element method of lines for moving interface problems with
nonhomogeneous flux jump, Contemporary
Mathematics, 586(2013), 257-265.
n
He,
X., Lin, T., Lin, Y., Immersed Finite Element
Methods For Elliptic Interface Problems With Non-Homogeneous Jump Conditions,
Journal Of Numerical Analysis And
Modeling, 8(2011), 284-301.
n
Adjerid, S. and Lin, T., A
p-th degree immersed finite element for boundary
value problems with discontinuous coefficients, Journal of Applied Numerical Mathematics, 59(2009), 1303-1321.
n
He,
X., Lin, T., and Lin, Y., A
bilinear immersed finite volume element method for the diffusion equation with
discontinuous coefficient, Communications
in Computational Physics, 6(2009), 185-202.
n
He,
X., Lin, T., and Lin, Y., Approximation
capability of a bilinear immersed finite element space, Numerical Methods for Partial Differential
Equations, 24(2008), 1265-1300.
n
Adjerid, S. and Lin, T., Higher-order
immersed discontinuous Galerkin methods, International Journal of Information &
Systems Sciences, 3(2007), 555-569.
n
Lin,
T., Lin, Y., and Sun, W.-W., Error
Estimation of a Class of Quadratic Immersed Finite Element Methods for Elliptic
Interface Problems, Discrete and
Continuous Dynamical System, Series B, 8 (2007), 757-780.?
n
Camp,
B., Lin, T., Lin, Y., Sun, W.-W., Quadratic
Immersed Finite Element Spaces and Their Approximation Capabilities, Advances in Computational, (2006)24:
81-112.
n Kafafy, R., Lin, T., Lin, Y., and Wang, J., Three-dimensional immersed finite element methods for electric field simulation in composite materials, International Journal for Numerical Methods in Engineering, 2005, 64:940-972.
n
Li,
Z., Lin, T., Lin, Y., Rogers, R.C., An
Immersed Finite Element Space and Its Approximation Capability, Numerical Methods for Partial Differential
Equations, 20(2004), pp. 338-367.
n Li, Z., Lin, T., and
Wu, X., New
Cartesian Grid Methods for Interface Problems Using Finite Element Formulation,
Numerische Mathematik,
96(2003), 61-93.
n Lin, T., Lin, Y., and Rogers, R.C., and Ryan, L.M., A rectangular immersed finite element method for interface problems, Advances in Computation: Theory and Practice, Vol. 7, 2001, pp 107-114.
n
R.E.
Ewing, Z. Li, T. Lin, Y. Lin, The immersed finite volume element method for the
elliptic interface problems, Mathematics
and Computers in Simulation, 50(1999), 63-76.
Some
1D
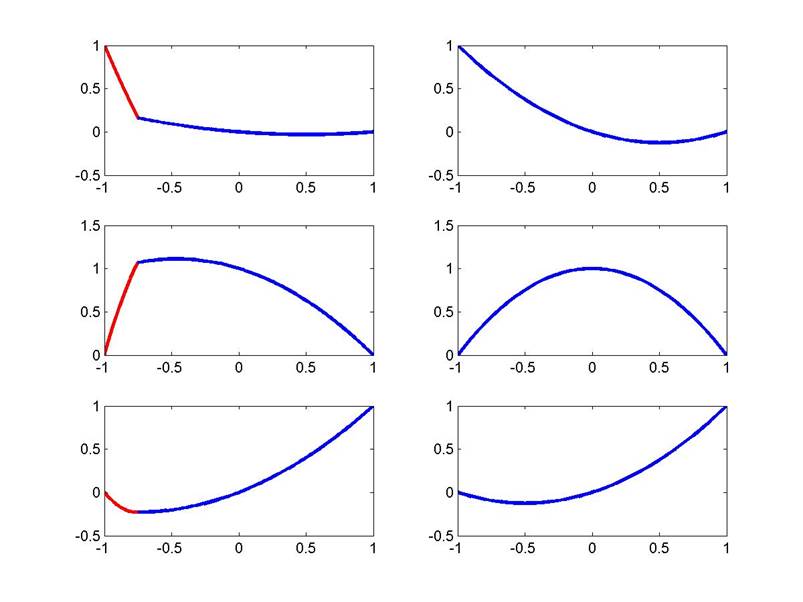
(a). Plots for
comparing the quadratic
The
plots on the left column are for the
and the plots on the right column are for the standard FE basis functions.
The
interface is located at -3/4 for these
(b). Matlab
code for the p-th (p <= 5) degree Lagrange type IFE
2D linear IFE
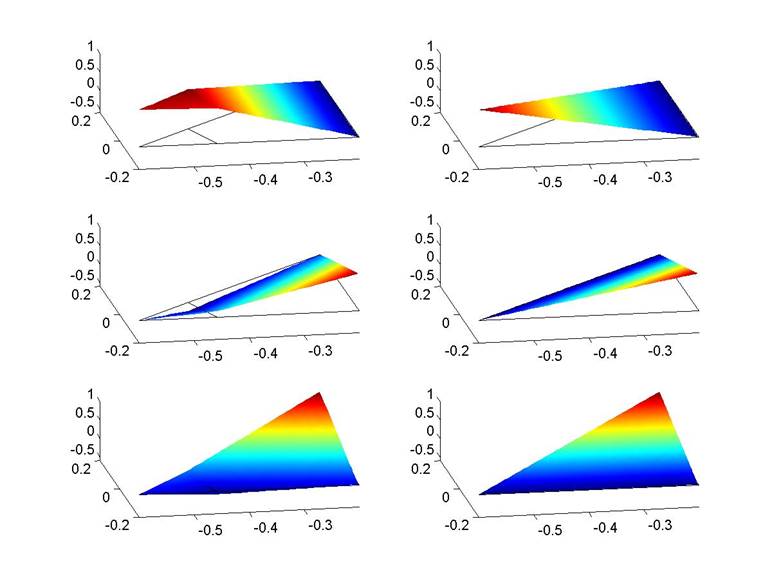
(a). Plots for
comparing the 2D linear IFE
The
plots on the left column are for the
and the plots on the right column are for the standard FE basis functions.
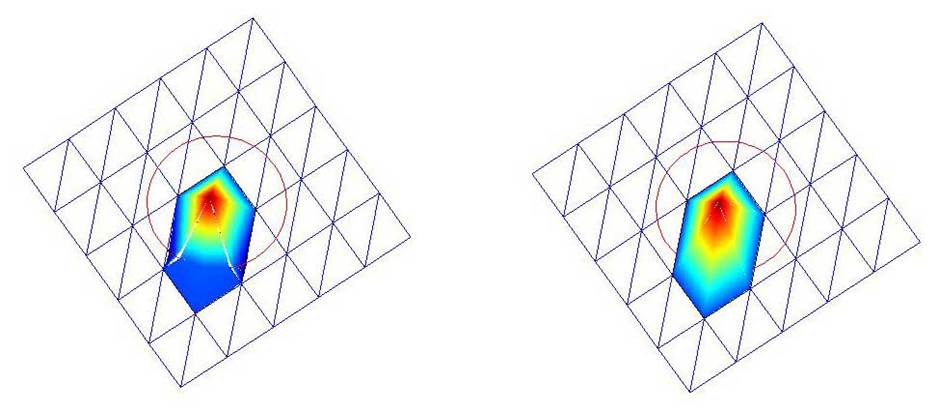
(b). A linear IFE
A linear IFE
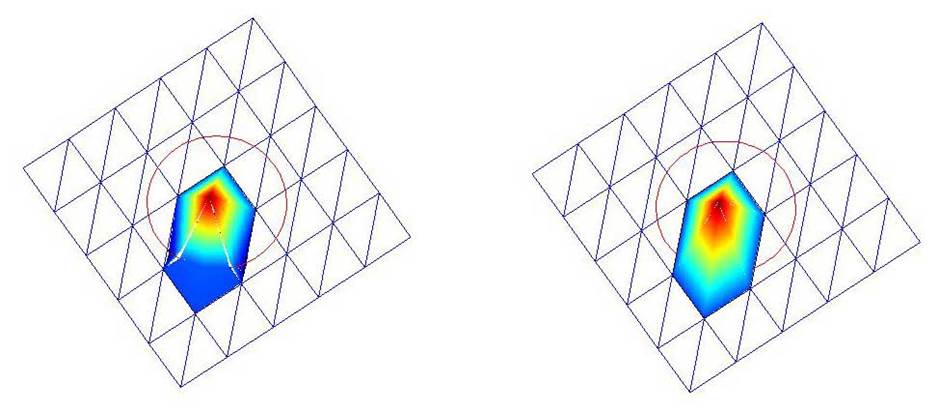
(c). Matlab can be used to see more details of the global IFE
basis above and the corresponding global FE function as follows:
n Download the fig file for the linear IFE
basis
n Download the fig file for the linear FE
basis
n Load these fig
files into Matlab as follows:
uiopen('ife_2D_linear_basis_global.fig',1)
uiopen('fe_2D_linear_basis_global.fig',2)
These Matlab commands will open two figure windows to display the
plots for the global basis functions. Then the plots can be rotated for more
details.
(d). Matlab code for the 2D linear IFE
2D bilinear IFE
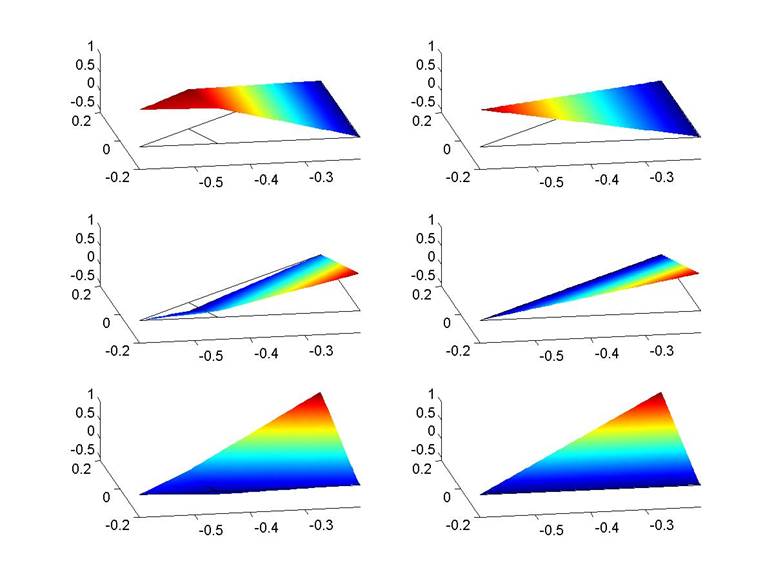
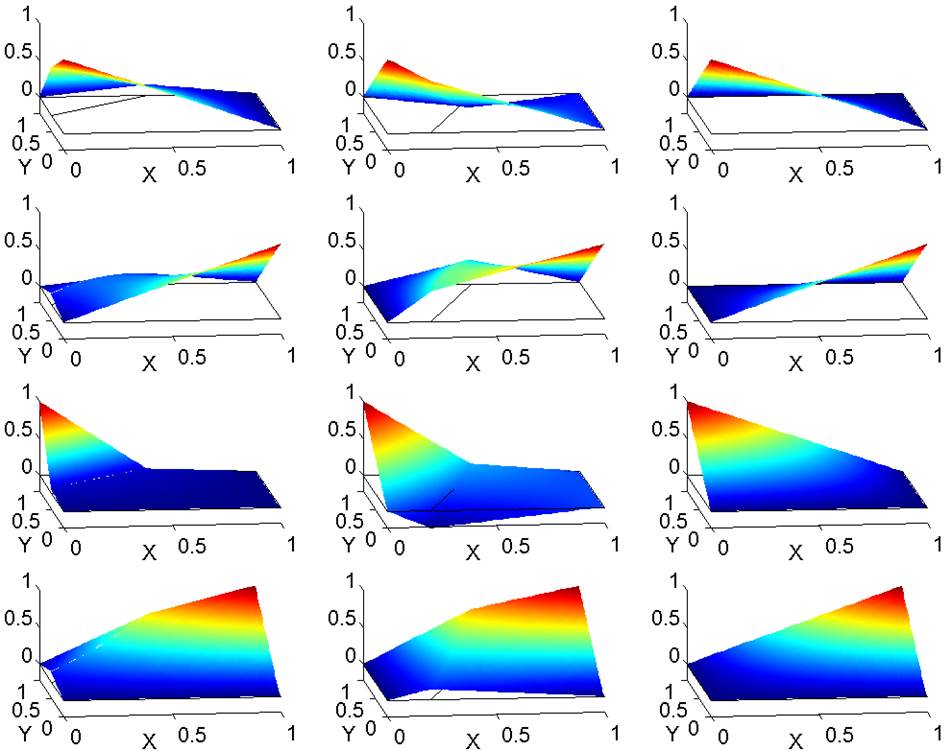
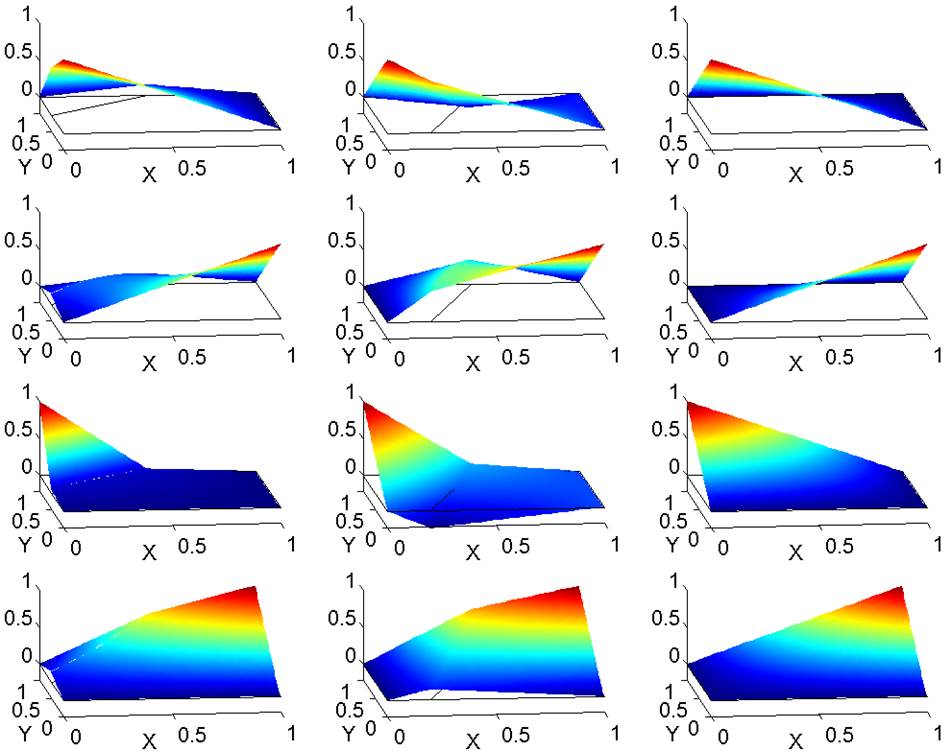
(a). Plots for
comparing the 2D bilinear IFE
The plots in the 1st column are for the Type I IFE basis functions,
the plots in the 2nd column are for the Type II IFE basis functions,
and the plots in 3rd column are for the standard FE basis functions.
(b). A bilinear
IFE
A bilinear IFE
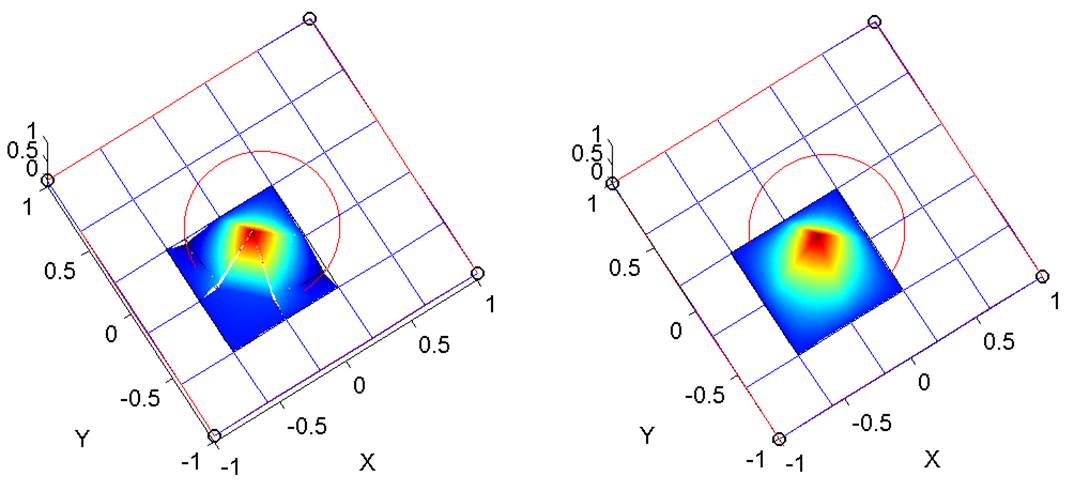
(c). Matlab
can be used to see more details of the global IFE basis above and the
corresponding global FE function as follows:
n Download the fig file for the bilinear IFE
basis
n Download the fig file for the bilinear FE
basis
n Load these fig
files into Matlab as follows:
uiopen('bilinear_ife_global_basis.fig',1)
uiopen('bilinear_fe_global_basis.fig?2)
These Matlab commands will open two figure windows to display the
plots for the global basis functions. Then the plots can be rotated for more
details.
(d). Matlab code for the 2D bilinear IFE basis functions (coming
soon)
Some
FE links:
Links
for inverse problems:
Research links from our department
Miscellaneous links