- Set
r = x2 + y2. Then
f (x, y) = ln(1 - r) - 1/(2r - (x + y)2),
so for given r, we see that f is maximized when x + y = 0.
Therefore we need to maximize
ln(1 - r) - 1/(2r) where
0 < r < 1. The derivative of this function is
1/(r - 1) + 1/(2r2) = (2r2 + r - 1)/(2(r - 1)r2)
which is positive when r < 1/2, 0 when r=1/2, and negative when
r > 1/2. It follows that the maximum value of this function occurs
when r = 1/2 and we deduce that
M = - 1 - ln 2.
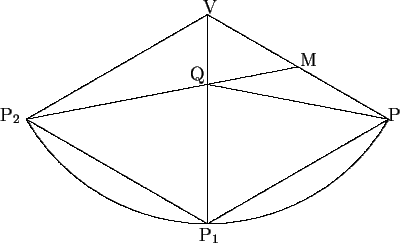
- We cut the cone along PV and then open it out flat, so in the
picture below P and P1 are the same point. We want to find Q
on VP1 so that the length of MQP is minimal. To do this we
reflect in VP1 so P2 is the image of P under this reflection,
and then MQP2 will be a straight line and the problem is to find
the length of MP2.
Since the radius of the base of the cone is 1, we see that the length
from P to P1 along the circular arc is
2p, hence the angle
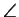 PVP1 is
p/3 because VP = 6.
We deduce that
PVP1 is
p/3 because VP = 6.
We deduce that
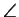 PVP2 = 2p/3,
and since VM = 3 and
VP2 = VP = 6, we conclude that
MP2 =
PVP2 = 2p/3,
and since VM = 3 and
VP2 = VP = 6, we conclude that
MP2 = 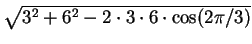 = 3
= 3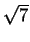 .
.
- We calculate the volume of the region which is in the first octant
and above
{(x, y, 0) | x>y}; this is 1/16 of the required
volume. The volume is above R, where R is the region in the
xy-plane and bounded by y = 0, y = x and
y =
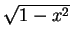 ,
and below
z =
,
and below
z = 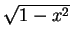 . This volume is
. This volume is
| |
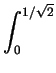 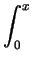 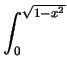 dzdydx + dzdydx + 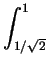 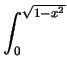 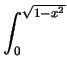 dzdydx dzdydx |
|
| |
= 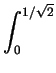 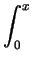 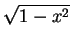 dydx + dydx + 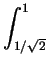 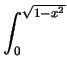 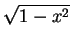 dydx dydx |
|
| |
= 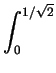 x x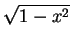 dx + dx + 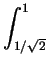 (1 - x2) dx (1 - x2) dx |
|
| |
= [- (1 - x2)3/2/3]01/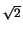 + [x - x3/3]1/ + [x - x3/3]1/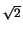 1 1 |
|
| |
= 1/3 - 1/(6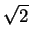 ) + 2/3 + 1/(6 ) + 2/3 + 1/(6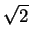 ) - 1/ ) - 1/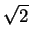 |
|
| |
= 1 - 1/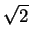 . . |
|
Therefore the required volume is
16 - 8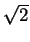 .
.
![\includegraphics [scale=.89]{cylinders.eps}](img14.gif)
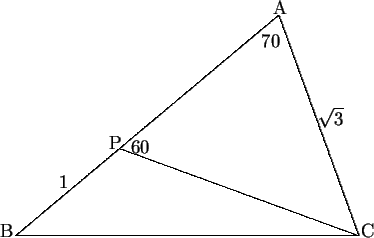
- We shall prove that AB = BC.
Using the cosine rule
applied to the triangle ABC, we see that
BC2 = AB2 + AC2 - 2(AB)(AC)cos 70. Therefore we need to prove
AC = 2ABcos 70. By the sine rule applied to the
triangle APC, we find that
AP = 2sin 50, so we need to prove
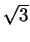 = 2(1 + 2sin 50)cos 70. However
sin(50 + 70) + sin(50 - 70) = 2sin 50cos 70,
sin 120 =
= 2(1 + 2sin 50)cos 70. However
sin(50 + 70) + sin(50 - 70) = 2sin 50cos 70,
sin 120 = 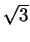 /2 and
sin(50 - 70) = - cos 70. The result follows.
/2 and
sin(50 - 70) = - cos 70. The result follows.
- Since
S1/an is a convergent series of positive terms, we see
that given M > 0, there are only finitely many positive integers n
such that an < M. Also rearranging a series with positive terms
does not affect its convergence,
hence we may assume that {an} is a monotonic
increasing sequence. Then
b2n + 1>b2n>an/2, so the
terms of the sequence {1/bn} are at most the corresponding terms
of the sequence
2/a1, 2/a1, 2/a2, 2/a2, 2/a3, 2/a3,...
Since
S1/an is convergent, so is the sum of the above sequence
and the result now follows from the comparison test for positive term
series.
- We shall assume the theory of writing permutations as a product of
disjoint cycles, though this is not necessary. Rule 1 corresponds to
the permutation (1 2 3 4 5 6 7 8 9 10) and Rule 2 corresponds to the
permutation (2 6)(3 4)(5 9)(7 8). Since
(2 6)(3 4)(5 9)(7 8)(1 2 3 4 5 6 7 8 9 10) = (1 6 8 5 2 4 9 10)
(where we have written mappings on the left) has order 8, we see the
position of the cats repeats once every 16 jumps.
Now 10p.m. occurs after 900 jumps, hence the cats are in
the same position then as after 4 jumps and we conclude that
the white cat is on post 8 at 10p.m.
![]() PVP1 is
p/3 because VP = 6.
We deduce that
PVP1 is
p/3 because VP = 6.
We deduce that
![]() PVP2 = 2p/3,
and since VM = 3 and
VP2 = VP = 6, we conclude that
MP2 =
PVP2 = 2p/3,
and since VM = 3 and
VP2 = VP = 6, we conclude that
MP2 = ![]() = 3
= 3![]() .
.

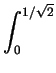
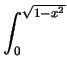 dzdydx +
dzdydx + 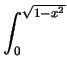
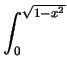 dzdydx
dzdydx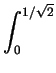
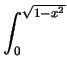
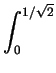 x
x![\includegraphics [scale=.89]{cylinders.eps}](img14.gif)
